GeekTry

# 3. 线性代数回顾

# 矩阵和向量

矩阵维度：行数x列数，左为4x2，右为2x3

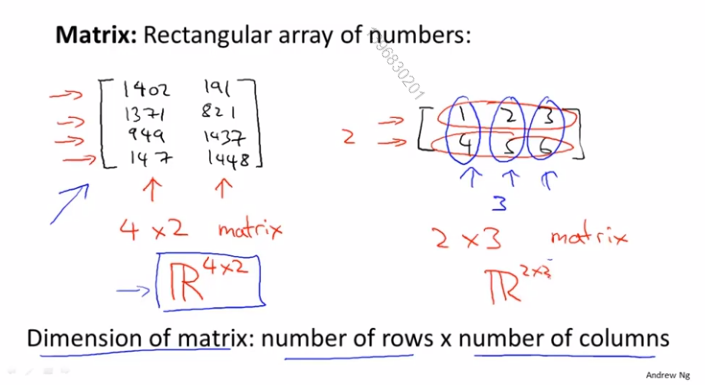
image-20200430141444601

矩阵元素：下标从1开始，A_11=1402，A_12=191

image-20200430141650673

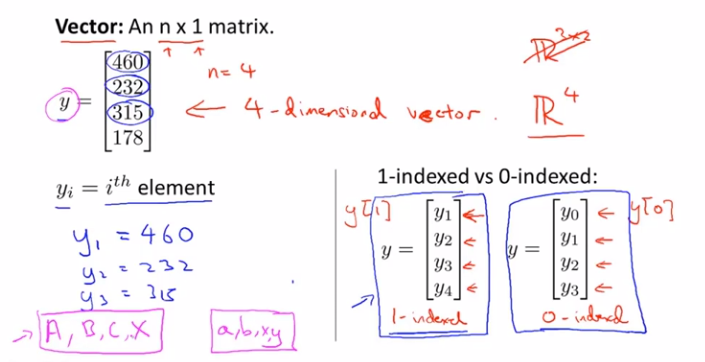
向量：一个n x 1的矩阵，y_1=460，下标从1开始比较常见

image-20200430141901312

# 加法和标量乘法

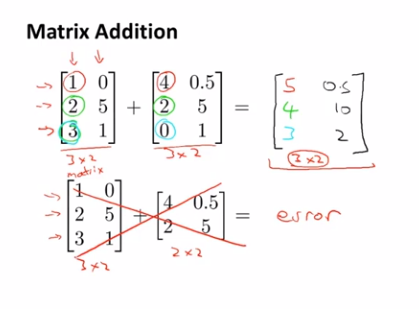
矩阵加法：只有同维度矩阵可以相加，结果也是与相加的两个矩阵维度相同的矩阵，每个相同坐标元素值相加的和即为新矩阵每个元素的值

image-20200430142130419

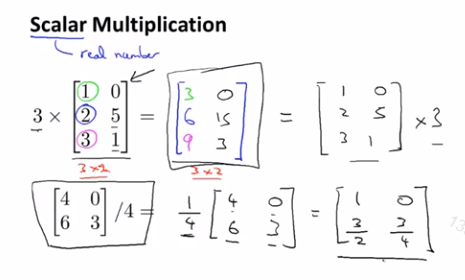
标量与矩阵的乘除法：

image-20200430142547483

复合运算：

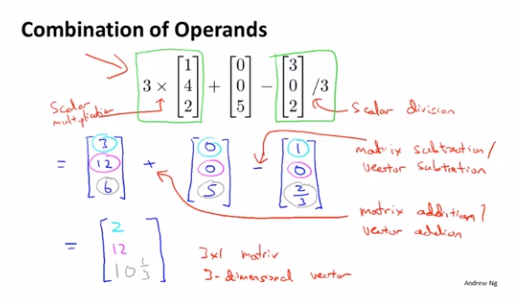
image-20200430142814485

# 矩阵向量乘法

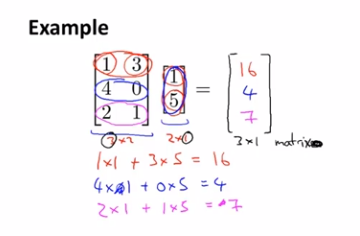
矩阵向量乘法：我们先来看一个3x2的矩阵乘以一个2x1的矩阵（或者叫2维向量）的例子。

这里得出的结果是一个3x1的矩阵（或者叫3维向量），其中3来自于被乘矩阵的行数，1来自于乘矩阵的列数，运算方法如下图

image-20200430143054920

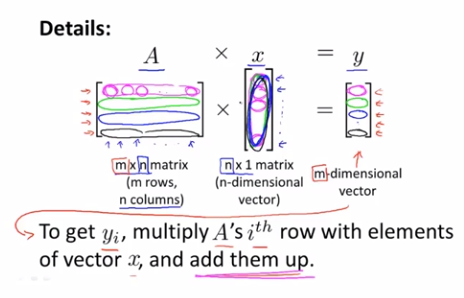
细节：只有当被乘矩阵的列数和乘矩阵的行数相等时，才能运算，方法是逐个计算y_i，最后合起来

y_i的值等于A中i行的第j个元素乘以x中第j个元素的累积和（j从1递增到n，步长1）
1

image-20200430143956514

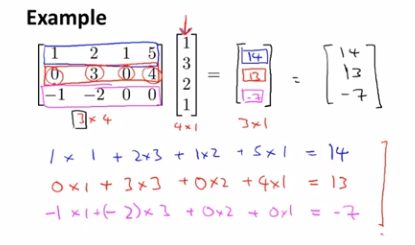
另一个例子

image-20200430144907086

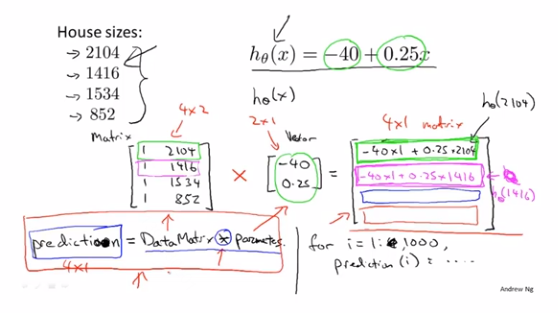
应用：prediction = datamatrix x parameters在预测房屋价格时，可以让计算过程简化成一行代码让计算机来完成，更高效

image-20200430145910460

# 矩阵乘法

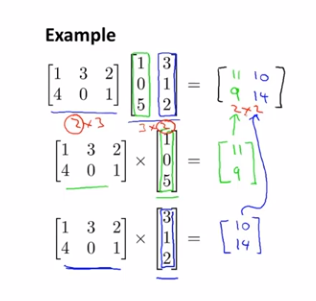
矩阵与矩阵乘法：和矩阵向量乘法类似，最后把结果合并即可

image-20200430150107230

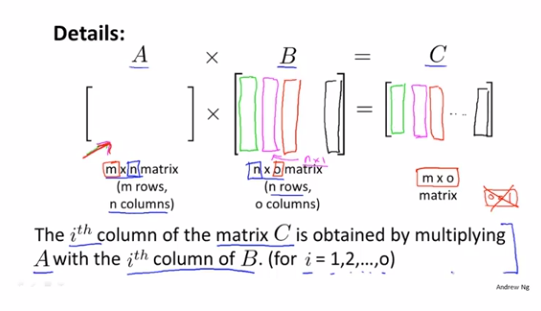
细节：与矩阵向量乘法类似，多一个结果合并的步骤

image-20200430150621901

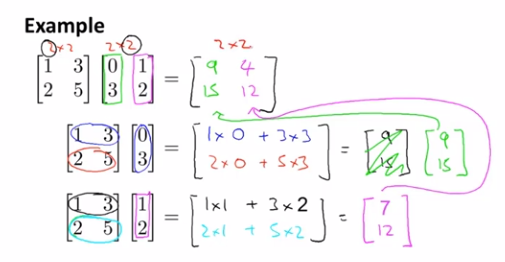
另一个例子

image-20200430150721418

应用：还是之前预测房屋价格，1次矩阵运算，得到基于3个假设函数对4个房屋面积预测到的价格

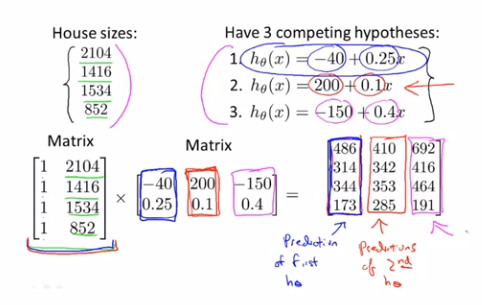
image-20200430151027416

# 矩阵乘法特征

矩阵乘法不满足交换律（not commutative），交换后所得结果矩阵维度并不一定相同，即使维度相同，矩阵元素位置和值也不一定相同

image-20200430151542569

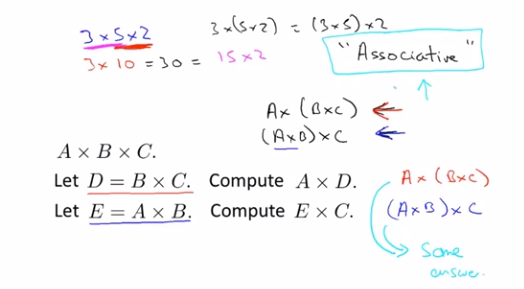
矩阵乘法满足结合律（associative）

image-20200430151818507

单位矩阵（identity matrix），记作I，相当于实数中的1，单位矩阵乘以任何矩阵等于任何矩阵本身，且满足交换律

image-20200430152109040

# 逆和转置

逆矩阵：只有方阵有逆矩阵，方阵为m x m维，一个方阵和自身的逆矩阵相乘，等于单位矩阵I。元素全为0的方阵没有逆矩阵，没有逆矩阵的矩阵也称作奇异矩阵（singular）或退化矩阵（degenerate）

image-20200430153052355

转置矩阵：将原矩阵以45°对角线反转，即为原矩阵的转置矩阵

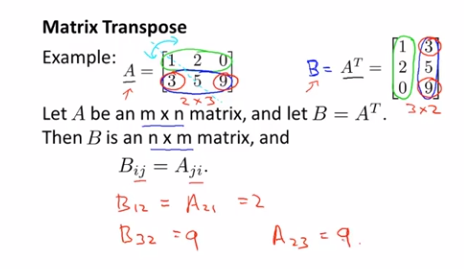
image-20200430153154460

最近更新: 7/5/2021, 2:29:57 PM

← 5. 多变量线性回归 →