# 2. 单变量线性回归
# 模型描述
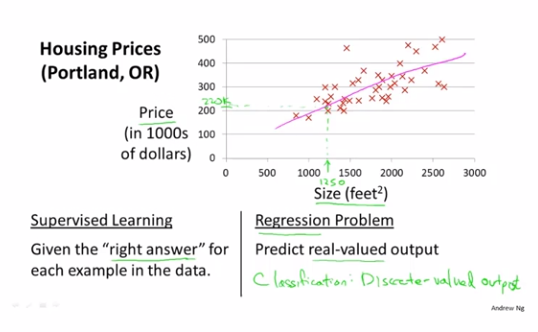
x轴为房屋面积,y轴为房屋售价,我们现在需要根据这些数据来预测当我们有个1250平方英尺的房子能卖多少钱?
我们可以做模型拟合,大致得出售价约为220000美元左右
这是一个监督学习算法的例子,因为每一个例子都有一个正确答案
这还是一个回归问题(regression problem)
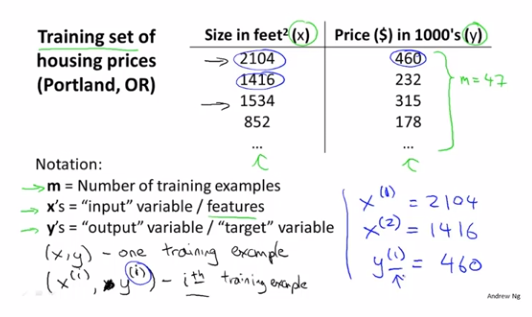
训练集(training set):m表示训练样本的数量,x表示输入变量,y表示要输出变量
(x, y)表示一个训练样本
(x^(i), y^(i))表示第i个训练样本(i从1开始)
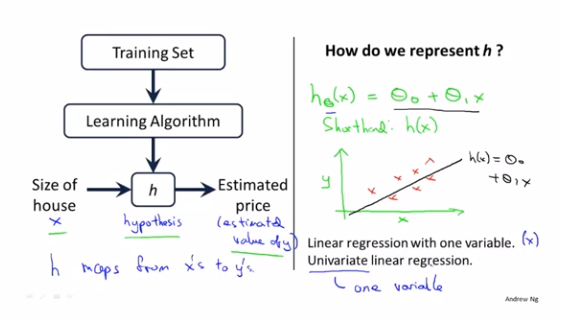
我们向学习算法提供一个训练集,学习算法的任务是输出一个假设函数h(hypothesis),h的作用是通过x来预测y
h_θ(x)=θ_0+θ_1*x
线性回归(linear regression)
一元线性回归(linear regression with one variable)
单变量线性回归(univariate linear regression)
# 代价函数
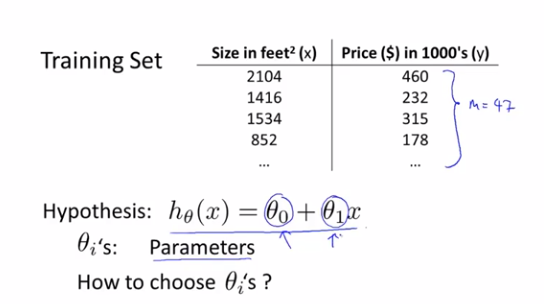
关键是如何选取θ_0和θ_1
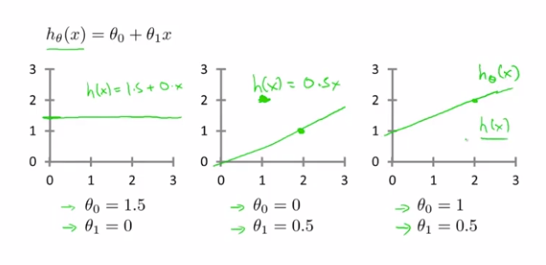
我们要做的就是得出θ_0和θ_1这两个参数的值,让假设函数表示的直线,尽量地与这些数据点很好的拟合
那么我们就要使h(x)也就是输入x时我们预测的值y最接近该样本对应的y值,这样的θ_0和θ_1就是我们需要的
所以我们要解决的是一个最小化问题(minimization problem)
简单来说,我们把这个问题变成了:
找到能使训练集中预测值和真实值的差的平方的和的1/2m最小的θ_0和θ_1的值
(取1/2m而不是1/m的原因是,后面求偏导数的时候能和平方的倒数抵消,方便计算)

代价函数(cost function)也叫平方误差函数(squared error function),或平方误差代价函数(squared error cost function)
平方误差函数对于大多数问题,特别是回归问题,都是一个合理的选择,可能也是最常用手段
# 代价函数(一)

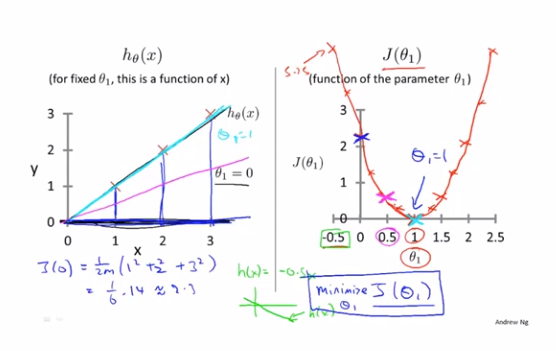
我们先简化假设函数,令θ_0等于0,即h_θ(x)=θ_1*x,给定训练集[(1,1),(2,2),(3,3)],想用代价函数J(θ_1)求出最小θ_1。通过对θ_1的不同取值,我们可以根据训练集得到不同的的J(θ_1)值,得到其图像最低点(1,0),即可以找到我们需要的最小θ_1,即为1,最后代回我们的h_θ(x)=θ_1*x,可得h_θ(x)=x,就是我们最终拟合的结果假设函数了
# 代价函数(二)

假设函数、参数、代价函数、目标
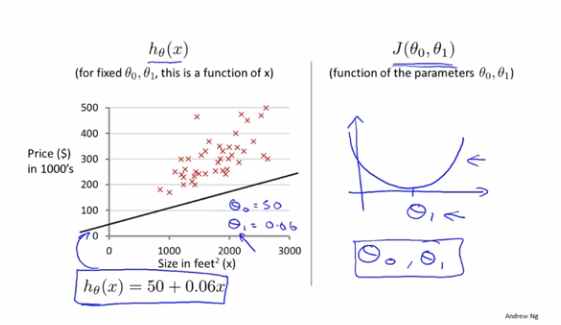
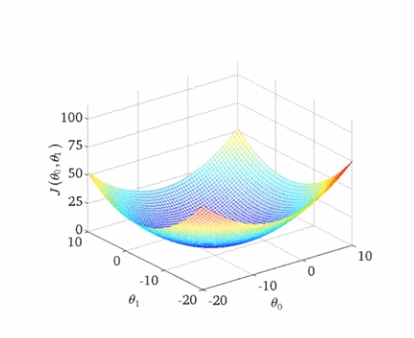
当我们有2个参数θ_0、θ_1的时候,代价函数J(θ)的图像就会是个3D的碗状图形
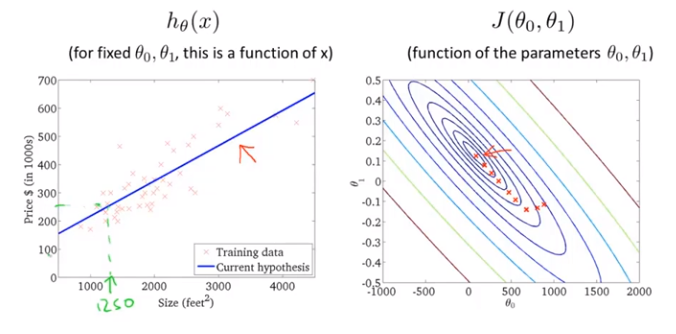
等高线图(contour plots)或等高图像(contour figures)
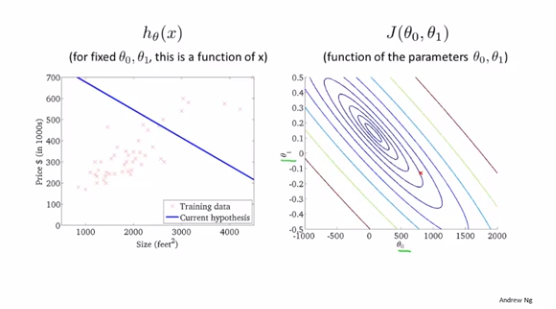
右图中每个圈代表的是J(θ_0,θ_1)值相等的点
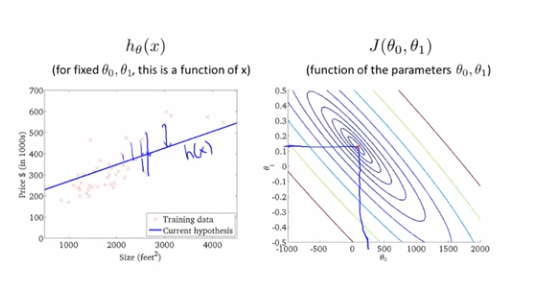
越靠近圆心的点所对应的点(θ_0,θ_1)能更好地确定假设函数h_θ(x)来拟合当前训练集的点分布情况
# 梯度下降
梯度下降是很常用的算法,它不仅被用在线性回归上,还被广泛应用于机器学习的众多领域

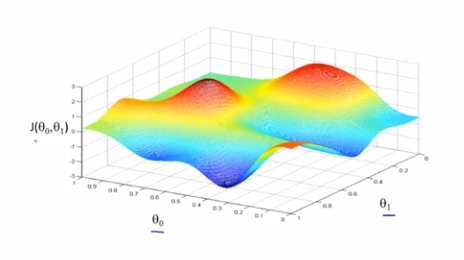
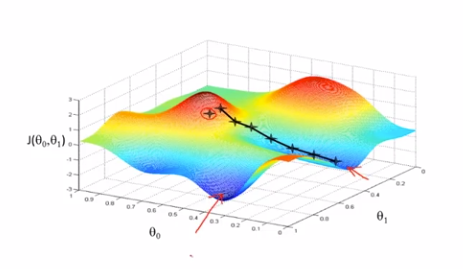
不同的初始值(θ_0,θ_1)设定,有可能让梯度下降找到并不相同的局部最优点

这里需要注意的是,θ_0,θ_1需要做到同步更新
# 梯度下降知识点总结

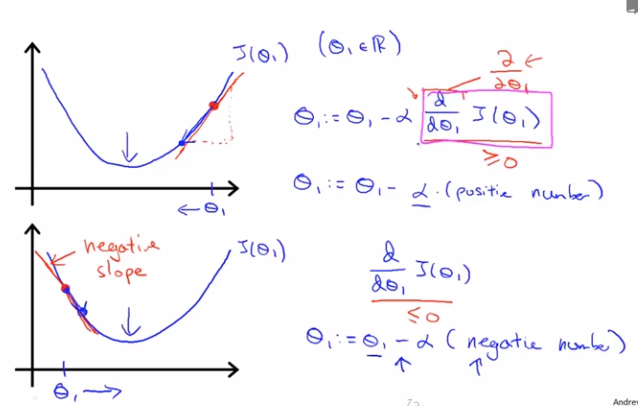
式中α为学习速率,α后面的项为代价函数J(θ_1)在θ_1方向上的偏导数,也可以看成斜率
如果当θ_1取值在最低点的右侧,J(θ_1)在该点偏导数为正数,新的θ_1必减小(靠近最低点)
如果当θ_1取值在最低点的左侧,J(θ_1)在该点偏导数为负数,新的θ_1必增大(靠近最低点)
所以θ_1值最终都会收敛
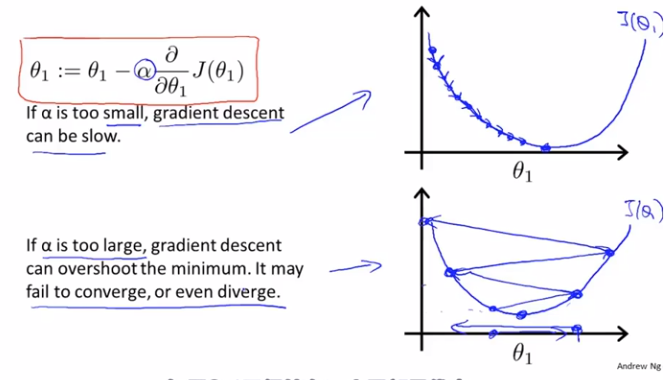
当然,如果学习速率α取值过大,就会发现θ_1值无法收敛甚至发散
那么,如果θ_1已经在一个局部最优点,下一步梯度下降会怎么样?
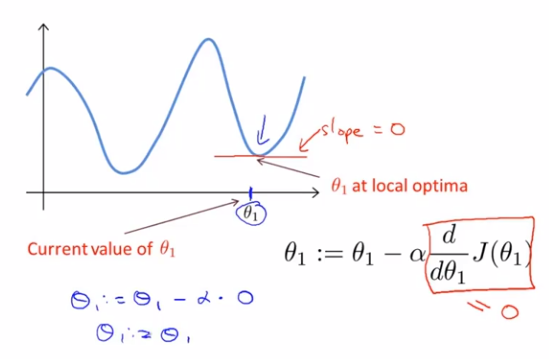
该点偏导数为0,θ_1将不会再被更新
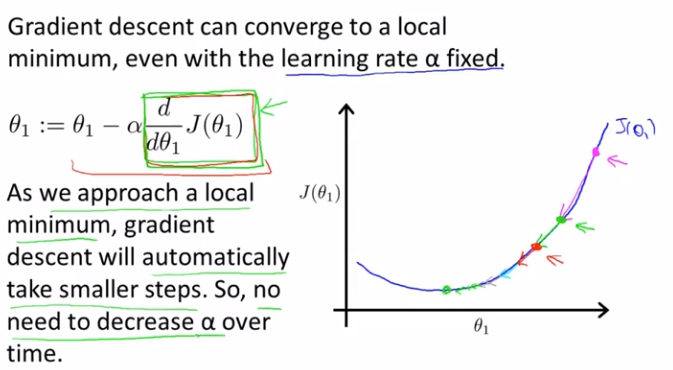
此外,当我们越接近局部最优点时,偏导数会越来越小,每次θ_1减去的值也会越来越少,所以我们没有必要去减小学习速率α了
# 线性回归的梯度下降

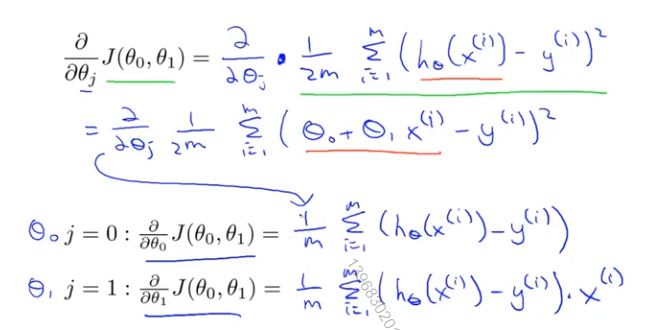
这里需要令h_θ(x^(i))-y^(i)=t,用链式法则可解

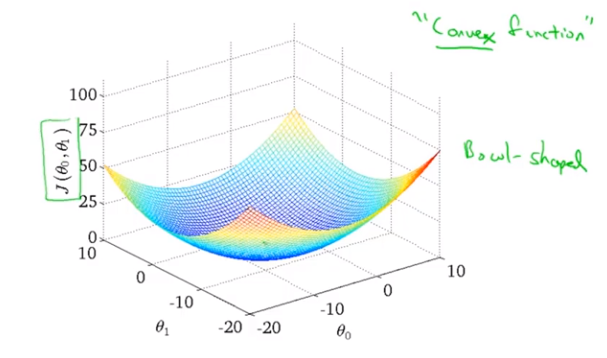
大部分情况下,都为凸函数(convex function)或弓形函数(bow-shaped function)

有时候称此算法为Batch梯度下降("Batch" gradient descent)
意味着每一步梯度下降,都遍历了整个训练集的样本
正规方程组方法(normal equations methods)
